2018年7月17日 星期二
何謂慣性? 慣性定律?
『慣性』即為所有物質皆有的某種性質,就像遊戲中出現『火屬性』的字樣,馬上點出此物品或此人物擁有遇到水會收到兩被傷害的性質一樣。所以說只要提到『慣性』我們也可以了解一個物質在某些特殊狀況下會展現出這樣的特性。
非常、超級、很不巧的是,慣性這種性質是所有物質皆有的,更正確地說,只要有質量的東西都會具有這樣的特性。
慣性的特性文言文說明版本如下:物體保持原來運動狀態的特性。
好,讓我們開始翻譯翻譯什麼較『保持』什麼叫『原來運動狀態』。
先讓我們看看以下精美的圖示
沒有錯,這張圖就是A、B兩個人站在馬路的兩側,很明顯的兩人在空間的位置上並不同。這張圖既自然又生動,展現了平凡無奇的日子當中城市內的一隅。
但如果是下面這張圖。
慘,這兩個人都是A,實在是太詭異了。可能A會影分身之術,又或者A擁有自己的克隆人,不然畫面中不會出現兩個A。還好旁邊的註解讓一切變得自然,左側的A是凌晨三點整的A,右側的A是3點零一分的A,我們先姑且不論為什麼這個傢伙會在凌晨三點過馬路,至少時間的附註讓我們得知,左右兩個A在時間與空間上面有差異,講白話文就是:A過馬路。
好了,為什麼要特別花篇幅特別解釋一個過馬路的人呢?因為只要不是瞬間移動,一個物體在不同時間出現在不同空間就是物理上的『運動』這樣的運動一定要具備一個東西,不可能沒有,就是『速度』。
在A沒有超能力也不會法術的狀況下,除了速度,你不可能解釋為什麼A會在一分鐘之後出現在另一邊。好吧,也可能是幻術。但總之速度這個要素說明了運動的可能性。
讓我們回到文言文:保持原來運動狀態
所以『原來的運動狀態』指的就是原本的速度。讓我們再看以下精美的圖示。
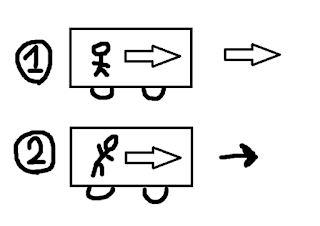
圖1是一個人在搭公車,公車高速前進,所以由車外的觀察者來看,車內乘客的速度也是隨著公車高速前進的,如果速度沒有隨著公車一起前進,那很有可能是他沒趕上這班公車,老司機可是說開就開的,離題了。
圖2是車子剎車,所以車子的速度變慢了,但是車內乘客在那個瞬間『保持原來的運動狀態』也就是維持原本的速度在前進,原本的速度是還沒有減速的狀態,所以比較快,因此當車子已經慢下來了,結果你還在用剛剛的高速往前,就會有往前傾倒的現象。
所以你看,這就是慣性。當然乘客最後也會跟著車子一起慢下來,但在"改變"的過程中,人這個物體趨向於維持原來的『運動狀態』
最後再用文言文說明慣性定律: 在不受外力的情況下,一具有質量的物質,具有保持原來運動狀態的特性。
相信了解慣性的文言後,對於這邊慣性定律應該多多少少有所明白,簡單的說,在物質有慣性的情況下,只要不要有人去戳它、踢它,或對它做出任何有"交互作用"[1]的行為,物體是不會隨便改變它的運動狀態的,也可說它是不會隨便改變它的"速度"的。
舉凡剎車時人會往前傾倒、拍棉被讓塵埃脫落[2],這些東西都是因為具有質量的物質們遵守著慣性定律,其他慣性定律的例子自己google。
註解區
[1] 交互作用:詳細請看"交互作用"的文章,但我還沒寫,呵呵
[2] 棉被被你拍走了,塵埃還"維持原來運動狀態",也就是靜止(速度等於零),人家棉被都走掉了,塵埃還停在那邊,自然兩者分離的狀況,塵埃因重力就往下掉了。當然也有可能是你打得很大力,另一方便塵埃直接被你拍飛。
2018年6月12日 星期二
科學這些事,說起來肚子餓了還是得吃飯
眼前那些形形色色的平凡事跡,腦內自動忽略原本該注意的科學
話說,又有誰會嘗試去思考每一件事呢?
燈號轉為小綠人的那刻,大學生拎著便當走向對街的校園,手機上的時間──5:30。
大概是接下來有社團活動,五點半也不能算是早食,某些人能在這個時間就意識到自己是餓的,但誰也沒注意到,胃酸竟然含有少量鹽酸的成份。就說了,人不會把每件事都拿去Google,到頭來最後靠的還是問題的發生。
嘛,就算知道了也對人生沒什麼影響嘛。是的,如果你的人生是能被偶然知道的小知識所改變,你大概不是什麼簡單的人物。每天一杯珍奶對人的影響遠大於知曉一則新知,畢竟比起知識的膨脹,身體的膨脹係數還是比較大而明顯的。
所以咧?所以有人將這些思考排除於他的生活之外,也是呢,當喝著星巴克的咖啡人們會想思考的應該是人生吧,總不會是『啊,這豆子產地是蘇門答臘』,如果有的話,農場主人會哭的唷,會落下好幾十年來終於有人懂他的眼淚。
但也許就是這樣,一種不但不神秘而且近乎無聊的新鮮感誕生了。它的神祕感就像主廚的神秘配方,消費者只關心CP值,只有主廚自己在那邊神秘。而這些述說著"鉛球和羽毛會同時落地"的言論像是前菜,後面還有一堆不好意思端出來的理論基礎,怕你吃不下。
我是科學的美食獵人,是個只懂得品嘗前菜的美食評論家,可以告訴你哪個開胃,剩下是要填飽、還是求得一品佳餚,這還得看你怎麼點餐。科學就是一鍋熬了千年的大骨湯,就只等帶LNG開台。
2017年5月20日 星期六
第四維?
<關於座標>
『XXX在哪?』要怎麼描述一個人或一個物體切確的位置呢?
『我在台北車站,東邊,三公尺處』就是一個清楚的表達方式
當一句話含有 參考點(台北車站)、方向(東邊)、距離(三公尺處)
有了這些資訊我們就可以得到物體的位置。
再舉一個例子:你到前面紅綠燈右轉,大概再騎三分鐘就到了
『你到前面紅綠燈(參考點)右轉(方向),大概再騎三分鐘就到了(距離)』
(這邊的三分鐘是用時間乘上一般認知的車子速度得到距離)
雖然有了明確表達位置的方式,但只有這樣是不夠的,所以引進了『座標』
用二維座標來看台北車站這個例子
畫出一個二維座標,十字的中心(原點、參考點)就是台北車站,座標軸中的每一格都代表一公尺,所以當目標物出現在東邊第三個點上,一樣可以清楚的得到『我在台北車站,東邊,三公尺處』這個資訊。除了用語言描述的方式,也可以直接畫一個座標圖,看到座標圖的人一樣可以很快的清楚物體的位置。
利用座標點的表示法,更能夠快速的知道一些比較難表達的位置,比如下張圖
要怎麼描述綠點位置呢?如果用一般口語的描述會是:
『大概在台北車站的東北方』(模糊板)
或『台北車站往東走三公尺,再往北兩公尺』(清楚板)
但如果是用座標來表示,只要明定X的正方向為東,Y的正方向為北
則物體的位置就在
(3,2)
的位置。所以座標就超方便的,座標本身就把『參考點、方向、距離』涵蓋在其中了,最後要表示物體的座標,只要在兩個維度上面 (X,Y) 給定XY 其位置座標馬上就可以知道物體在哪了。甚至於利用"向量"可以有更多靈活的運用(不贅述)
<座標小結論>
要清楚第四維度為什麼要先講座標? 因為要先知道什麼是一維、二維、三維
而"空間"在有些部分其實是抽像難以簡單描述的,所以利用座標可以將空間量化
化為一些線條,這樣也比較好想像。
如同古時第谷和克卜勒等人是如何記錄星體位置的? 當然也是利用座標,將天空畫上虛擬的線條,並記錄這些數字。看著數字,就可以在腦內翻譯出星體位置。
<維度與數學>
先看一張圖
依照前述,要表達綠點位置可以以 (3) 來表示,而藍點可以使用 (-4) 表示。
因為在一維座標當中,僅有兩個方向,所以括號內只有單一數字。如果是二維可能就會有如前面所說的 (3,2) 這種表示方式。那如果是三維呢?
(3,8,-4)、(5.2 , -71 , 0.235) 三個數字在括號中,其表達分別為 X Y Z 三個維度。
而這些數字是可以化為"向量"做計算的。
比方說你現在往天空丟一顆球,最後落下的地點在哪? 只要有足夠的資訊,這些都是可以被記算出來的。
當維度的表示利用座標的數學呈現後,就成為了可計算的東西。
<三維生物>
所以我們這些活在三維生物的人可以計算並且繪畫,畫出一維空間的樣子,比如一條繩子,又可能是一張2D的場景美術圖,比我們低維度的都可以輕易的操作。
當然三維可能要多費一些功夫,像是3D列印出的模型,使得你在每個位置每個角度,都可以看到模型不同的樣貌。
但二維生物就沒這麼幸運(如果有二維生物的話) 低維度世界是無法看得到較高維世界的。
舉個例子:在紙上畫出一個火柴人,這個火柴人他可以隨意的在紙張上亂走,但也因為他是二維的生物,所以他無法跳脫這張紙,但我們三維生物就不同了,我們可以把這張紙舉起來,或把它放在地板上。對我們來說,因為紙張的"高低"不同了,自然紙上的火柴人"位置"也會有變化,但如果你有機會問火柴人,火柴人可能會告訴你『我沒有動啊? 我從頭到尾都沒動,我的"位置"沒有改變』為什麼他會這麼說? 因為它無法感受到第三維。
兩個座標(3,2,8)、(3,2,-1)火柴人能感受能知道的只有他在(3,2)無法辨別第三個數字(也就是第三個維度) 這就是低維無法用直觀的方式描述、畫出、感受高維度的原因。
在星際效應的電影當中,為了涉及 "三維與四維" 的說明,科學家卻是拿了一個"二維的紙"作示範,為什麼? 就是因為我們三維生物是無法感受到 四維、五維,所以才會用二維物體與三維空間(科學家所在空間)來示範,用這樣的方式讓人們自己去想像 三與四之間的關係。
以上的"感受"皆指 人體、肉體的感官,比如"看到" "摸到" 等等
<計算高維>
那怎麼辦? 身為三維生物,要怎麼延伸討論到四維五維?
還記得前面講座標那邊嗎,雖然我們無法直接用我們三維生物的器官去感受這些,但是我們有數學。
會不會我們也像二維生物一樣只感受到前面幾個維度 (3,2,8) 其實有第四個 (3,2,8,31) 之類的呢? 有的,答案一樣是數學。
講"數學"可能有點太廣義,如果要細分的話,可能是結合不同領域科學的數學,比如弦論、量子力學..等等,這些不同的領域用以計算高維度,當然所得到的意義也會不同。
<所以說,什麼是第四維?>
第四維有兩種討論方式,第一種一樣就是所謂的空間,也就是說在現有空間中、我們所在的空間中,其實一直有第四個維度(也是空間維度之一)只是我們就如同那個火柴人一樣,當把這張"紙"放在不同"高低"的時候,我們斯毫無法靠人體感官去感受。如此一來我們只能用三維的方式去模擬四維、五維... 等等高維度的空間,如同星際效應最後出線的超立方空間。
第二種,愛因斯坦為了探討時空,所以將第四維設為時間,藉此探討了狹義、廣義相對論。對於時間是第四維的想像,也讓很多科幻作品有了"時空穿越"的想像。
所以"第四維" 是要討論時間,還是空間呢?
兩種討論方式走向不同的方向
如果是要討論穿越時空的話,當然是少不了時間了。
2015年12月5日 星期六
奧伯斯悖論─思考宇宙的起源
 |
| wiki: Milky_way |
如果宇宙是張沒有邊際的圖畫紙,要畫幾顆恆星才夠?那些已知和未知的恆星充滿宇宙,閃耀的光芒經過數個光年的距離來到地球,從恆星的光我們看到了過去。但思考到這不禁想問,若宇宙是亙古無窮的,找不到起始點更沒有終點,宇宙一直『存在』,數不清的恆星分佈在其中,會不會眾多恆星的光芒使天空失去了黑夜?
 |
| 每個方向的視線都對應得到一個恆星 |
夜裡只要抬頭仰望,天空的每個區塊不論多遠都找得到恆星對應的話,眼前的視野將會被宇宙中無窮的恆星所照亮。事實是,每天晚上抬頭所看到的天空都是黑夜,那要怎麼解釋看得到黑夜的事實呢?為了思考這個問題產生了許多對於宇宙的想法。
 |
| 然而星體本身也並非永恆的,有生有滅 |
『如果宇宙不是無窮的而是有起點的...』打破宇宙永恆存在的說法,恆星有限的存在於視線之中,更尤其有了起點,也許只是那些光還沒到達罷了,人們所能見的僅只是某段有限時間內的歷史而已。
那麼宇宙又是怎麼開始的?遙遠地方的恆星在這有限的宇宙中是否在遠離我們?
-----
補充:
關於圖三,這是其中一種思考脈絡的示意圖,並非真實宇宙的狀況,所以要拿來跟真實宇宙狀況比較的話會有許多錯誤存在。
2015年9月28日 星期一
【國中理化】力矩 (重點提醒)
本篇僅講解在國中理化中,力矩所需要注意的地方
假設大家已經讀過力矩的章節以及算過一些題目。
1. 力矩 = 力臂 x 力?
公式大家都會背,但這裡的力臂指的是"有效力臂"
何謂有效力臂 (有笑?)
先來看一張一點都不有效的力臂
左側為固定端,中間有根桿子,右側有個力量F用水平方向的力量拉扯
桿子根本不會旋轉對吧,因為有效力臂為零
我們嘗試用別的力量方向,再來畫出有效力臂試試看
藍色的線條不是桿子,實際生活上你看不到那條藍藍的線
藍線就是所謂的有效力臂
有效力臂 = 從固定點出發畫到垂直於F方向的長度
比如藍線與桿子的夾角是37度,而桿子剛好是5公尺
所以有效力臂就是4公尺
(藍線黑線與紅線中間的三角形是個3、4、5的直角三角型)
若F = 8N
力矩 = 4*8 = 32
最後看一般最常看到的狀況
桿子和力量F方向本身就是互相垂直的
圖型就像這樣
因此畫出的有效力臂剛好等於桿子長
這也是為什麼多數題目可以直接用 "桿長乘以力量F"的原因
2. 力矩平衡
若一個系統力矩平衡,那麼就要定好
"所有讓桿子逆時針轉的力矩 " = "所有讓桿子順時針轉的力矩 "
3. 力平衡 + 力矩平衡
看一下這個圖
我先給一個完整公式再來解釋
F1 = F2 + F3 ...... (1)
F2 * R1 = F3 * R2 .......... (2)
式子(1) 指的是力平衡,也就是之前所學的靜力平衡
因為系統保持靜止,所以所有往上抬升的力量會等於往下的力量
式子(2) 就是力矩平衡 ,R1、R2無庸置疑就是力臂
當列出這兩個式子,就得到一組聯立方程式
大致上這類型的題目就可以解決
2015年9月26日 星期六
月曆上的數學
『重要的日曆缺了一部份,被遺忘的月份將會被盛大地弔唁 ..... 』
(摘自"畫到你孫子的孫子都出生了還是畫不完"作品)
在月曆上可以發現一些有趣的事,本篇不囉嗦,直接來看有哪些吧!
1. 每過七天(或7的倍數天)剛好會是同一星期
以2015年的九月每個星期六為例子:
九月的5、12、19、26號,都是星期六
而這些數字間剛好都差七的倍數
比如 5號與 12號差了7天、12號與26號差了14天
為什麼同一星期剛好會差七的倍數呢?
因為一週剛好就是七天,學過因數倍數的你想想看怎麼回事吧!
2. 同一年的 4/4、6/6、8/8、10/10 剛好是同一星期
以2015年為例,4/4、6/6、8/8、10/10 都是星期六
這個巧合怎麼來的呢? 不是巧合是數學!
我們把 4/4與6/6 標示在數線上,同時也把5/4、 6/4也標上
因為我們發現 4/4~5/4剛好經過一個小月(30天)的時間
而5/4~6/4經過一個大月(31天),這樣一小一大剛好會是61天!
然而我們要找尋的6/6就是比原來的4號多兩天,再加上2就是63天
63剛好是七的倍數,如此一來再利用第一點所說的:
"相隔7的倍數天,一定會是同一星期"
得到4/4與6/6一定會是同一星期。
同理可推 6/6 ~ 8/8 也是相隔一個大月和一個小月,然後再外加兩天。
最後,利用以上的說明,來找找看 12/12是不是也是星期六吧!
補充知識:
若x月有N天,從x月y日要到x+1月y日,剛好會經過N天
2015年6月24日 星期三
高中物理: 功與動能 - 『碰撞』題型觀念整理
(延續上一章節力學能守恆本篇討論的是功與動能章節中的碰撞)
【觀念整理】
兩個具有質量的物體相撞會發生什麼事情?
"彈性碰撞" 與 "非彈性碰撞"!
彈性碰撞:碰撞時,動能沒有轉變為其他型式的能量
非彈性碰撞:有轉變 (例如轉成熱能的型式)
若非彈性碰撞中,原來動能完全轉換成其它能量型式
就會變成 "完全非彈性碰撞"
若我們用一個由0~1稱為恢復系數的數來表示碰撞情形
恢復係數e與碰撞的關係可表示成:
彈性碰撞 e=1
非彈性碰撞 0<e<1
完全非彈性碰撞 e=0
以下這邊開始是本章重點
[1] 彈性碰撞公式
 |
| V1、V2皆為碰前;V1‘、V2‘表碰後速度 |
是的,如果你現在要準備的是段考,就先努力的背下來這個公式吧!
建議背法:先將黑色的部分記起來,因為上下兩個公式寫起來很對稱
較不容易寫錯,再來紅色的部分就看你要用什麼絕竅去記憶,譬如:
V1‘是1號的地盤,所以在V1區是 1-2 、V2區是兩倍的m2
V2‘是2號的地盤,所以在V1兩倍的m1 、V2區是 2-1
[2] 接近速度等於遠離速度
彈性碰撞公式背不起來沒關係,因為彈性碰撞公式就是從以下三個式子來的
(1) 能量守恆:前動能總和 = 後動能總和
(2) 動量守恆:前動量總和 = 後動量總和
(3) 由以上兩個守恆所推導出的 『接近速度=遠離速度』
第一、二式守恆的條件前面已經學過了,而第三式能使用的條件是彈性碰撞
從這三個式子就能推導出[1]的彈性碰撞公式,所以忘了也沒關係
還是可以利用這些我們學過的東西求得碰撞結果,不過若能背下彈碰公式當然最好。
我們直接看個例子
一質量m的球以V的速度撞擊2m靜止的球;
假設兩者進行的是彈性碰撞,求碰後兩者速度?
若用彈碰公式可直接求得m球速度為 -(1/3)V,因為是向後所以速度為負
2m碰後速度為(2/3)V。
若用"動量守恆"與"接近速度等於遠離速度"
可列出以下:
(1) mV + 0 = mV1‘ + 2mV2‘
(2) V - 0 = - (V1‘ - V2‘)
解聯立就可以得到V1‘ 和 V2‘
[3] 完全非彈性碰撞
因為完全非彈性碰撞考的反而比非彈性碰撞多
所以直接討論完全非彈性碰撞。
完全非彈性碰撞因為動能轉變為其他型式,所以無法用前後動能守恆來做題
更無法用彈性碰撞公式來解決,但是通常題目都會是系統無外力作用的狀況下
簡而言之就是可以使用 動量守恆來著手解題。
【各個題型】
1. 二維彈性碰撞
二維彈性碰撞和上一節處理動量一樣分成X與Y討論
2m球與靜止之m球彈性碰撞,m球與水平方向夾角37°射出
求2m球碰後速度V1與m球碰後速度V2為多少?
[X部分] 一樣用彈碰公式或使用動量守恆可求得V1x與V2x
[Y部分] 因為有了V2x可以利用三角函數得到V2與V2y
最後V2y會與V1y動量守恆,推得V1
2. 衝擊擺 - 完全非彈性碰撞
一個衝擊擺可以測試出子彈的速度,至於怎麼測?
看到下面這個題目:
子彈質量m射入質量M木塊內,木塊擺至h的高度
以知重力加速度為g求子彈的速度為何?
首先假設子彈速度是v
然後依力學能守恆可以寫出....
是的這樣答案就出來了
重點就在於要分成兩步驟進行
第一是求得木塊擺上去前的速度
再來由動量守恆得到原速 (當然也有可能反著考你高度多少)
3. 質心速度
 |
| 紅花不見的原因是被壓過去了 |
在一個充滿小草的光滑無摩擦的平面上 ...
好啦我知道有小草不可能光滑無摩擦,手上有綠筆誰都不能阻止我畫小草!
總之上面有一個質量m的木塊以速度v撞擊一個質量M的斜面 (彈性碰撞)
斜面也是光滑的,過程中木塊最高爬升垂直高度是h
問爬升到h時m與M的速度為何?h是多少?木塊離開斜坡後速度為何?
(1) 當木塊爬升到最大高度的時候,木塊相對斜面是靜止的
所以木塊跟斜面都會以質心速度向前移動。
質心速度 vc = mv/(m+M)
(2) 依能量守恆
(1/2)mv^2 = (1/2)mvc^2 + mgh
↑整理上式即可得到h
(3) 可以直接想作是m與M的碰撞
求m的彈性碰撞碰後速度即可。
好吧整理就到這邊,記得在以上幾題當中學得的觀念
瞭解這些觀念為什麼可以在這邊使用?
為什麼會想到下一步是這麼作?
瞭解之後才能用這些觀念去解更多沒看過的題目
也不要忘了先前所學的物理觀念,才不會被綜合題型問倒。
訂閱:
文章 (Atom)